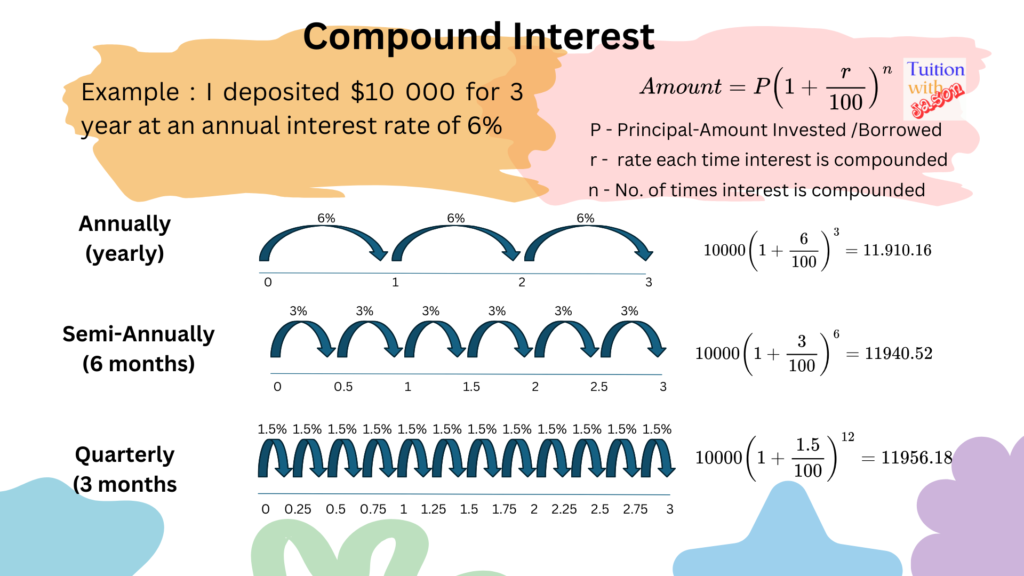
To illustrate Compound Interest, I used an example where $10,000 (Principal) is invested for 3 years at an annual interest rate of 6%. Below are three scenarios showing how the total amount differs when interest is compounded annually, semi-annually, and quarterly:
- Compounded Annually:
- Principal (P): $10,000
- Interest Rate (r): 6% per year
- Number of Compounding Periods (n): 3 (once per year for 3 years)
- Compounded Semi-Annually:
- Principal (P): $10,000
- Interest Rate (r): 3% per half-year (since 6% is the annual rate, divided by 2)
- Number of Compounding Periods (n): 6 (two half-years per year over 3 years)
- Compounded Quarterly:
- Principal (P): $10,000
- Interest Rate (r): 1.5% per quarter (since 6% is the annual rate, divided by 4)
- Number of Compounding Periods (n): 12 (four quarters per year over 3 years)
- As the compounding frequency increases (from annually to semi-annually to quarterly), the interest is calculated and added more frequently.
- This means the principal grows faster because each compounding period includes interest on the interest earned previously.
- Comparing the total amounts:
- Annual Compounding: $11,910.16
- Semi-Annual Compounding: $11,941.63
- Quarterly Compounding: $11,956.01
The difference may seem small for a short period like 3 years, but over longer periods or larger investments, the effect of more frequent compounding becomes significant.
Additional math (a-math), math (e-math) O-level, N-level sec 1, 2 and 3 math tuition at boon lay, jurong west and woodlands.
.